Characterisation of film-developer combinations
Resolution, edge sharpness, halo: methodology
The Siemens Star
The reference pattern I use is a Siemens star, a structure etched in chrome on glass. The outer diameter is 24 mm, the circle is divided into 36 uniform wedge-shaped pairs. In the centre there is a circular metallised area with a diameter of approx. 140 µm on which the metallic segments end.
The number of line pairs per millimetre (LP/mm) varies with the radius, from 80 LP/mm on the inside to 2 LP/mm on the outside. Figure 1 shows a microscopic image of the star on the left, the side length of the square is about 1.8mm. The circular section is given by the aperture of the microscope. The image on the right shows an enlarged view of the central area. For comparability with the images of the star on negative film to be analysed, these images are inverted.
Fig. 1: Microscopic image of the central area of the Siemens star. Left image: approx. 1.8 x 1.8 mm, right image: an enlargement of the central area. The pixel size of the image corresponds to 0.67 μm in the object plane.
The star can only be transferred optically to the film using the direct contact method. Using a lens to project the image would have a massive impact on the results due to the imaging performance of the lens and the precision of the focus.
During the contact process, it is important to ensure that the film is as flat as possible and that the star with the metallised side is placed directly on the film. The exposure has to be done in such a way that no artefacts, i.e. under-exposure and half-shadows, occur due to the unavoidable minimal distances between the light-sensitive layer and the metallisation of the star.
The film was laid flat by being inserted into a film cassette with a precisely fitting mask. The film lies on a glass plate and is pressed from above by the mask. The siemens star is placed in a recess of the mask, whose narrow side corresponds to the diameter of the star, with the metallisation facing the film. Due to the stops in the film cassette and the precise fit of the star into the mask, this can be done reproducibly in complete darkness without any problems.
The film was exposed using the light cone of a enlarger (Durst Laborator 900 with CLS 450). The lens aperture was completely closed at f=16, and the brightness was additionally attenuated by a factor of 8 using a neutral density filter. At a lens focal length of 50 mm and f/16 aperture, the diameter of the aperture is approx. 3 mm. At an illumination distance of 900 mm, this illumination is virtually a point source. A simple geometric consideration shows that at a distance of 0.05 mm (conservative estimate) from the light-sensitive layer to the metallisation of the star, the radius of the half-shadow is 0.17 μm compared to a width of 12 μm of the finest light-dark structure of the star and the optical resolution of the microscope of approx. 2 µm.
Optical transfer of the star onto the film
Exposure time and film processing
The metallised structure of the star represents an object of extreme contrast: the metal surfaces are opaque (D =∞), while the glass has a very high transparency
(D ≈ 0). The film zones behind the metallic surfaces are therefore not exposed and should show the grey fog of unexposed film throughout. The density behind the clear zones of the star can be varied by adjusting the exposure time. For a normally exposed and developed negative of an object with a typical contrast range (ΔΕ= 1.5), the density for bright objects that should still show detail is typically in the range of a film density of D = 1.0 - 1.3; see the page about density curve and film speed.
The contact exposure of the stars was chosen so that the exposed wedges in the outer area have a density in the above-mentioned range D = 1.0 - 1.3. The exposure curves were measured (D vs. Ε) for all film-developer combinations analysed and the development parameters were selected so that they are practical, i.e. the maximum steepness in the range D = 1.3 is approximately γ = 0.7-0.8, the mean steepness is approximately β=0.5-0.6.
EIt should be noted that a ‘lighting contrast’ cannot be specified here because the metallised areas (opaque) do not lead to any exposure. The difference between the unexposed grey value (typically D = 0.2-0.3) and the selected light density can be used as a measure of the contrast range on the film. This corresponds to a difference of ΔD = 1 or, with β = 0.6, a minimum illumination contrast of ΔΕ = 1.7, i.e. a factor of 45. Some manufacturers specify the resolution power for an illumination contrast of ΔΕ=3, i.e. a factor of 1000. Such a contrast would lead to film densities of D > 2.5 when developing film in the normal way for practical purposes. On the one hand, this is close to the saturation density of a normal negative film, but on the other hand, it leads to a massive loss of resolution of fine structures due to blooming (optical and chemical diffusion). It remains unclear how this manufacturer's information is to be understood.
Digitisation of the Siemens star images
UIn order to analyse and evaluate the depicted siemens stars, the methodology used must not significantly distort the results. Initial attempts to enlarge the negatives of the stars onto paper using the usual positive technique and then to examine them proved to be unusable because the resolution of the enlarging lens used (Rodenstock Apo-Rodagon 2.8/50mm) is worse than the resolution of low-sensitivity films. This is an example of how the investigations, at least in some areas, are of a purely academic nature.
The evaluation using a microscope and a smartphone to register the microscope images proved to be useful. Despite initial scepticism, it turned out that a simple ‘student microscope’ (brand BEBANG) is perfectly adequate for the magnification levels required here. All images were taken with a 4x lens and 25x eyepiece, i.e. at 100x magnification. The resolution of the microscope is approximately 2μm.
BWhen using a smartphone to digitise images, it is important to note that under no circumstances should the normal photo software be used for this purpose, as it edits the images in a variety of ways. This is particularly important if the images are to be evaluated not only visually but also numerically. The ‘Halide’ app was therefore installed, which allows images to be taken in RAW format with manual exposure control. This ensures that the images of different negatives can be evaluated under comparable conditions and without post-processing. The magnification was determined for each series of images by taking a picture of an object micrometer; Figure 2 shows an example.
Fig. 2: Image of a stage micrometer for determining the magnification. The fine scale is 10μm, i.e. 100 LP/mm. The entire image has 2750 x 2750 pixels, i.e. one pixel corresponds to 0.66 x 0.66 μm in the object plane. The image also illustrates the optical resolution of the microscope.
Visual analysis/observations
Figure 3 shows three examples of microscope images of siemens stars transferred to film, Figure 4 shows a magnified section of the central area.
Fig.3 : Siemens stars transferred to contact on film. Section approx. 1.8 x 1.8 mm. Ilford Delta 400 developed in Rodinal (left), XTOL (centre) and Wehner/Alpha (right).
Fig.4 : Siemens stars transferred to film in contact. Section approx. 0.35 x 0.35 mm. Ilford Delta 400 developed in Rodinal (left), XTOL (centre) and Wehner/Alpha (right).
Figures 3 and 4 show the effect of different developers on the same film (Ilford Delta400). When developing in Rodinal (left images), the distinctive grain structure is a limiting factor for the resolution and sharpness. Developing in XTOL (middle images) provides significantly finer grain structure, but here the decrease in contrast, i.e. the bright stripes becoming darker towards the centre, is clearly visible. The development in Wehner/Alpha takes a middle position: the grain structure is reduced compared to Rodinal, the contours appear more accentuated than in XTOL, the contrast reduction towards the centre is significantly less pronounced. The algorithmically determined limits of resolution (for the methodology, see next section) are shown as circles and are quite similar in all three cases
To demonstrate that the method used here of directly transferring the star to the film optically is not methodically limited (at least for films intended for pictorial shots), the star was transferred to a document film (SPUR Ultra R 800) using the same method and this was developed in a developer optimised for this purpose (SPUR nanotech UR). The developer was adjusted to a medium sensitivity of about 25 ASA, dilution 1+24, 9 minutes at 25 C. The result shown in Figure 5 demonstrates that visually a significant decrease in contrast due to blooming and film grain can only be suspected at best. The resolution of such a film cannot be determined with the means used here. However, it clearly shows that the effects measured on normal films are limited only by the film itself and not by the methodology of the measurement.
Fig.5 : Siemens star in contact on SPUR Ultra R 800 documentary film developed in SPUR nanotech UR.
Numerical evaluation
Resolution limit
In addition to the purely visual assessment of the image of the stars, it should be possible to evaluate the microscopic images numerically and to derive some characteristic quantities from them. The following procedure has proven to be practical and sufficiently stable. Nevertheless, the visual impression of the image remains important; the numerical evaluation should complement it and in no way contradict it in the result.
As mentioned at the beginning, it is important that the images are available in RAW format without any post-processing and that the numerical values of the digitised images reproduce the brightness values unadulterated. For this purpose, the central area around the centre of the star was selected from the RAW files as 2800 x 2800 pixels and the RGB data were summed into a grey value. The typical pixel size was 0.6-0.7 μm/pixel.
EAn analysis of the images in the spatial domain, i.e. brightness as a function of the coordinate in the image, proved to be extremely difficult and error-prone. Although the visual assessment of the visibility of a structure, i.e. the processing by the eye and brain, seems simple, I could not find any reliable algorithms to reproduce this digitally. The Fourier transform method, i.e. a change from spatial to frequency space (more precisely, the spatial frequencies), proved to be successful. Here, optimal use can be made of the fact that the ‘star’ is a periodic structure that leaves a unique pattern in the frequency space. In addition, all 36 stripe pairs automatically contribute to the evaluation.
Although it is certainly possible to interpret a direct 2-dimensional Fourier transform, the following approach seemed more illustrative:
First, the centre of the star is located in the spatial domain.
then concentric circles are defined around this centre, with the radius determining the line density (LP/mm)
for 68 lines from 8 LP/mm to 75 LP/mm, the brightness values are read out with 1000 points on each line
These are Fourier transformed numerically (periodic continuation).
the strength of the correct periodic signal compared to the ‘noise’ of other frequencies is a measure of the significance of the structure
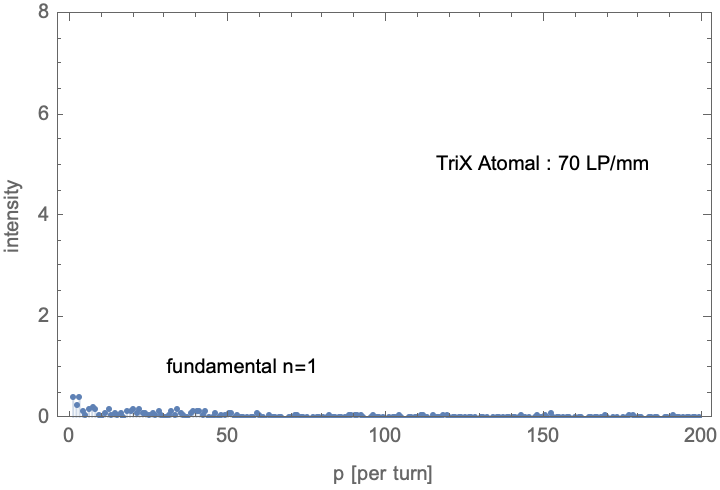
The following figures 6 and 7 show the Fourier spectra obtained in this way for the ‘reference film’ Spur Ultra R 800, a very good ISO 400 film-developer combination (Kodak TMY in Wehner/Alpha), and a rather poor combination (KODAK TriX in ADOX Atomal49), at 10 LP/mm and 70 LP/mm respectively.
Fig.6 : Spatial frequency spectra at 10 LP/mm for three different film-developer combinations. The signal at p = 36 per turn is the fundamental frequency of the star; the signals at 72, 108, etc. are higher harmonics. Explanations in the text.
Fig.7 : Spatial frequency spectra at 70 lp/mm for three different film-developer combinations. The signal at p = 36 per turn is the fundamental frequency of the star, the signals at 72, 108, etc. are higher harmonics. Explanations in the text.
The ‘signal’ at 36 per turn (pt) is the fundamental harmonic of the star, which consists of 36 light-dark segments. All three film-developer combinations show a very significant signal at 10 LP/mm. There are also higher harmonics, i.e. signals at double (n=2) and triple (n=3) the spatial frequency. These are explained in the next section. The ‘noise’, i.e. entries at false frequencies that have nothing to do with the periodic structure, are caused by the statistical light-dark fluctuations caused by the grain structure of the film.
The resolution limit of a film-developer combination can now be determined independently of visual assessment as follows: for all 68 circles, the signal strength of the fundamental harmonic is determined in relation to the ‘noise’, the signal-to-noise ratio S/N. This decreases with increasing line density according to a simple law (three free parameters) for all films, as shown in Figure 8. If S/N falls below a certain threshold, the periodic structure is no longer significantly visible, and the limit of resolution has been reached. Based on the comparison with the visual assessment of the microscope images, S/N=2 was chosen as the limit. This limit is arbitrary so that the absolute figures for resolution have a certain leeway, but not the comparison of the different films and developers with each other. The very simple parameterisation of the S/N dependence on the line density also allows resolutions to be determined by extrapolation that are (not too far) above the maximum line density of the Siemens star of 80 LP/mm.
For the reference film ‘Spur Ultra R 800’ (Fig. 8 left), S/N decreases very slowly from an extremely high value of > 100 at 10LP/mm; even at 80 LP/mm it is still > 30. Extrapolation to the limit S/N=2 is not useful here, it is definitely above 200 LP/mm. In this image, the decrease in S/N that is expected from the optical resolution of the microscope of approx. 2 µm is additionally shown as dashed blue and green lines. For this film, the values would have to be corrected, but for all the films in the analysis, this is not necessary because the correction is only very small.
The Kodak Tmax400 (TMY) in Wehner/Alpha developed (Fig. 8 middle image) achieves an extremely high resolution of >90 LP/mm for an ISO 400 film, the extrapolation is fairly uncritical here. At 80 LP/mm, the S/N is still more than 3, which allows for a very clean reproduction of the structure.
The classic Kodak TriX developed in ADOX Atomal 49 (Fig. 8 right image) is an example of a poor film-developer combination. The significance drops very quickly; above 45 LP/mm, the structure already disappears into the noise. For the comparative study, I did not consider ADOX Atomal 49 further because the results with other films are not convincing either.
Fig.8: Significance (signal to noise = S/N) of the periodic structure (blue dots, n=1) as a function of the line density for three different film-developer combinations. In addition, the S/N values for the harmonics with n=2 and n=3 are shown. See next chapter for explanation.
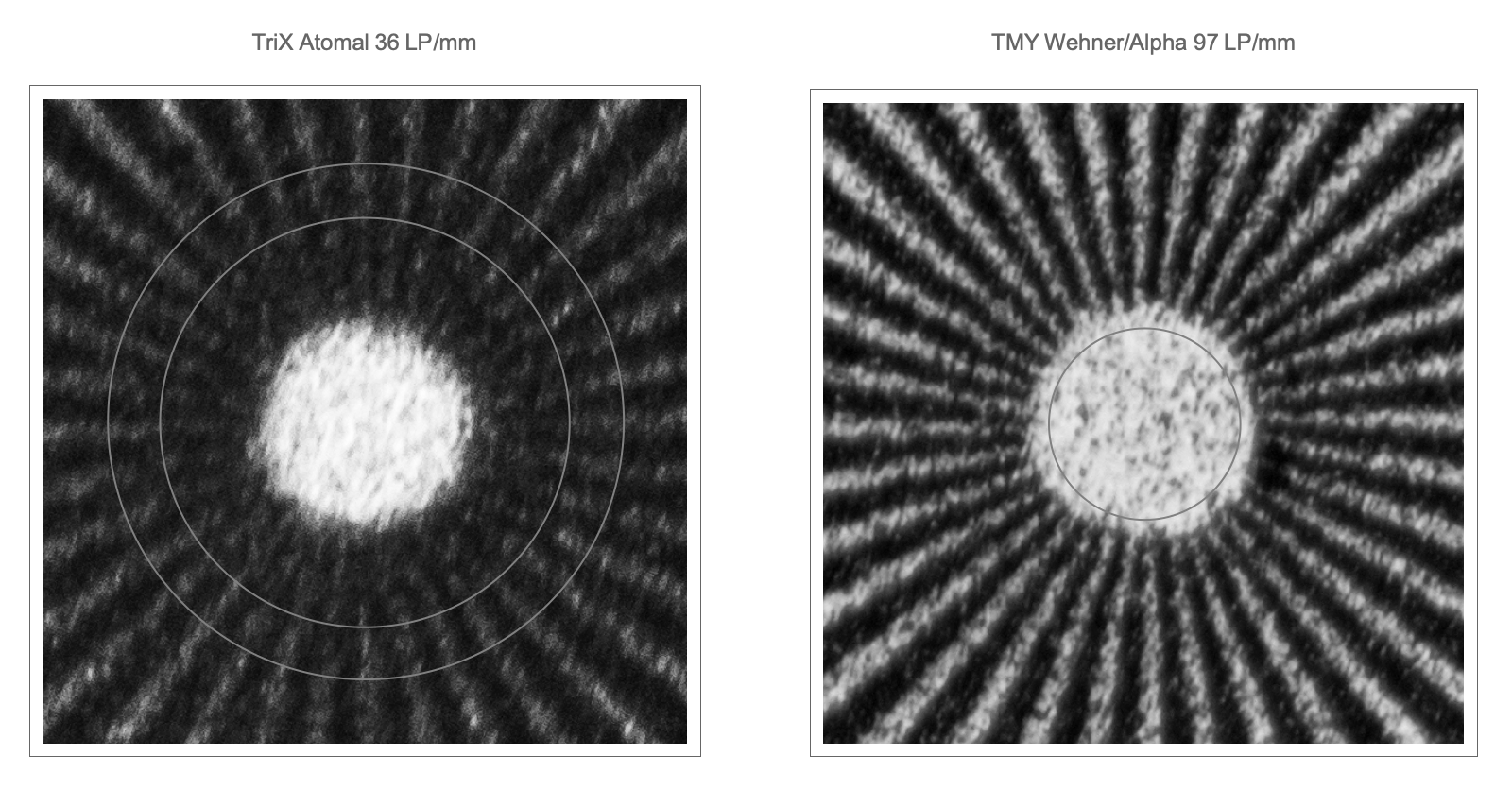
Fig.9 : Microscope images of the central area of the siemens stars for the two combinations TriX in Atomal49 and TMY in Wehner/Alpha. The grey circles mark the resolution limit as determined from the course of the S/N (Fig. 8).
The maximum resolution determined in this way may seem somewhat optimistic, and the S/N limit of 2 may seem too low. After all, a periodic structure is easier to recognise, even visually, than a single object. On the other hand, in the radial pattern of the star, only a very narrow range in radius is considered for a certain line density. It is therefore almost the resolution of a ‘point grid’. In a linear striped pattern, a large number of points with the same line spacing can be observed along the strip. The same applies to linear structures in the image. In this respect, the resolution limit defined here for line gratings can certainly be regarded as realistic.
InFigure 9 makes clear that the resolution limit can have different causes depending on the film-developer combination: for TMY in Wehner/Alpha, fluctuations due to the grain structure are the limiting factor; for TriX in Atomal49, the contrast disappears because the dark areas approach the light areas in their density. This phenomenon, the ‘growing’ of the dark stripes into the light areas, is what I call a ‘development halo’ or also an ‘halo’. The following chapter describes how this, as well as the edge sharpness, can be estimated from the parameters of the spatial frequency spectrum.
Edge sharpness and halo
Besides the fundamental harmonics, higher harmonics are also visible in the spectra (Figs. 6 and 7). This is because the periodic structure of the star is not a harmonic (sinusoidal) lattice with continuous light-dark transitions, but a strongly anharmonic sequence of sharply defined ‘exposed - unexposed’ segments. In the ideal case, i.e. for the star itself, it is a rectangular function whose Fourier series looks like this, where p is the period length:
$$h(s)=\frac{4}{\pi }\sum _{n=1,3,5}^{\infty } \frac{1}{n} \sin\left(\frac{2 \pi s}{ p} \right) $$
The square function with ideally sharp transitions therefore contains only uneven higher harmonics (n=3,5..), the strength of which decreases with 1/n. In our case of the base frequency 36 pt, these would be the lines at 108 pt, 180 pt, etc., which should have a strength of 1/3 or 1/5 of the base frequency. A reduced edge sharpness, a softer light-dark transition, is shown by the fact that the strength of the odd harmonics is suppressed. In Figure 6, left image, it can be seen that for the ‘reference film’ at 10 LP/mm, the amplitude ratio for the 3rd harmonic (n=3) of 1/3 is almost perfectly fulfilled, and the 5th harmonic is still very clearly visible. The small red circles mark the nominal values of 1/3 and 1/5. Figure 8 (left image) shows how the strength of the 2nd and 3rd harmonics decreases with increasing line density. In the ‘reference film’, the 3rd harmonic, the indicator of edge sharpness, can be measured up to the highest line densities, even if its relative strength decreases significantly from the ideal value of 1/3. Such an almost ideal behaviour can only be observed with this special film (very low sensitivity, very high steepness).
Besides the suppression of the odd harmonics, the appearance of a spurious n=2 harmonic is also observed. A possible cause for this is an asymmetry of the light-dark pattern, usually a widening of the dark (exposed) stripes into the light (unexposed) ones. The phenomenon can be referred to as halo, development fringes, or halation; it depends strongly on the developer used. Figure 10 shows the relationship with the n=2 and n=3 harmonics in a very simplified model of the ideal light-dark lattice. The left image shows the ideal line pattern. In the middle image, the n=3 harmonic is suppressed by a factor of 2 (the higher harmonics similarly), and the edge sharpness is significantly reduced. The right-hand image shows the case in which an n=2 harmonic occurs; the dark stripes are wider than the light ones.
Fig. 10: The meaning of the higher harmonics using a very simplified model as an example.
It therefore makes sense to define the relative strength of the n=3 harmonics $H_3$ at 8 LP/mm as a measure of edge sharpness; since the ideal value is 1/3, I define $SP = 3 H_3$ as a measure of edge sharpness. SP=1 corresponds to ideal sharpness, SP=0 to optimum rounding (sine).
If you look at Figure 8, you can see that the reference film has an almost optimal sharpness parameter (n=3), that of the very good combination TMY - Wehner/Alpha also has a very pronounced sharpness parameter at 8 LP/mm, but it is hardly measurable for TriX in Atomal. For the reference film, the value is SP = 0.92, TMY in Wehner/Alpha achieves SP = 0.73, while TriX in Atomal is SP = 0.21.
In a similar way, the relative strength of the n=2 harmonic at 8 LP/mm (for the experts: the real part of it) can be defined as a measure of the halo. From this, the width of the halo $B_h$ of the dark stripes can be estimated (in a very simplified model). Since the halo occurs on both sides of the dark stripes, the bright stripe disappears completely when the line density $LP > 1/(4 B_h)$.
Figure 11 shows the edge of the Siemens star for the three example films; the grey arcs indicate a line density of 8 LP/mm. The edge sharpness of the reference film is very high, with no measurable halo of dark stripes. The edge sharpness of TMY in Wehner/Alpha is still very good, with the halo determined to be approx. 2 µm. At TriX Atomal the edge sharpness is also visibly reduced, and the broadening of the dark stripe can already be clearly seen at 8 LP/mm, the halo is measured to be about 7 µm. This means that at 36 LP/mm the contrast should almost have disappeared; this limit is shown in Figure 9 as the outer circle.
Fig. 11: Outer part of the star for the three examples. The arc corresponds to 8 LP/mm.
While determining the resolution limit from the signal of the fundamental frequency is a very direct and clearly defined method, the parameters of edge sharpness and halo from the higher harmonics are rather indirect and therefore significantly less concise. However, comparability between different developers and films should be ensured.The following table contains all the parameters obtained from the Siemens stars for the 36 film-developer combinations in the comparative study.
A graphical representation of the numerical values can be found on the overview page, and a presentation of the relationships between the parameters on the page correlations.
The microscopic images of the centre and the edge area can be found together with the development parameters on the —> individual pages of the films.